Posets and Python 3 - Critical Group Diversion
- Jonathan

- Jun 22, 2023
- 8 min read
Updated: Jun 27, 2023
In our last post in this series, we implemented the Depth-First Search algorithm into Python as a function. What we'll do now is use that to add a method to our Poset class to return the maximal chains. As we've been doing, we'll add a "see = False" variable so that the method returns PosetElement objects unless we set "see = True", in which case we'll see their names.
class Poset():
...
def maximal_chains(self,see=False):
if see:
return DFS(self.get_elements(), self.get_relations())
else:
return DFS(self.set,self.relations)Check out that last post for the full code. Here are a couple of examples from last time, but within the poset this time.
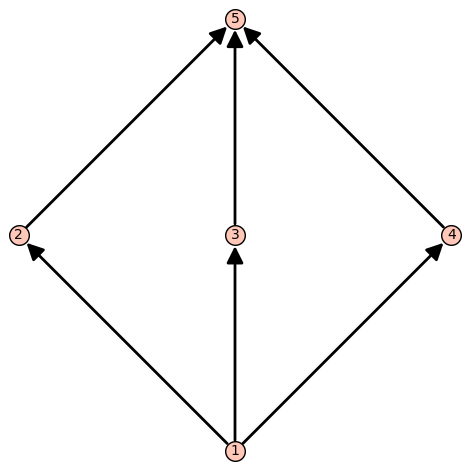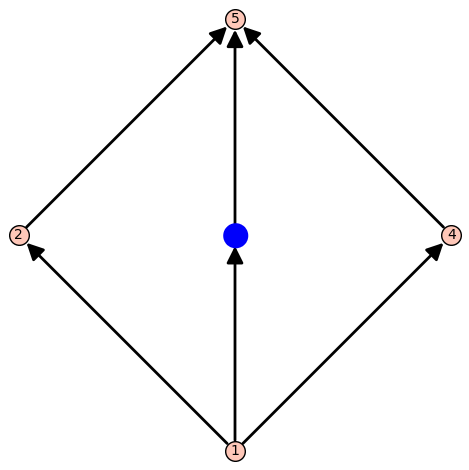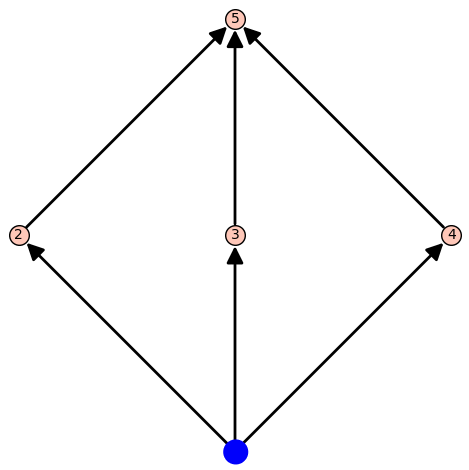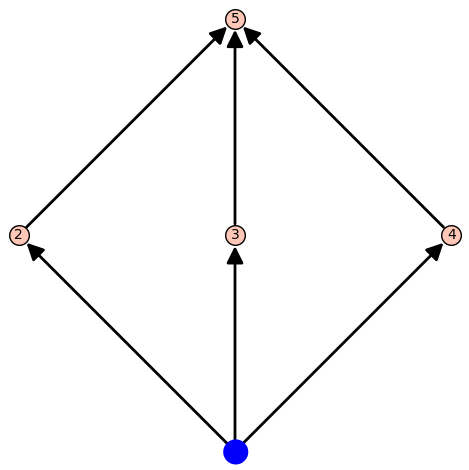
P = Poset([1,2,3,4,5],[(1,2), (1,3), (1,4), (2,5), (3,5), (4,5)])
print(P.maximal_chains())
#output: [[<__main__.Poset.PosetElement object at 0x10e0bf310>, <__main__.Poset.PosetElement object at 0x10e0bf3d0>, <__main__.Poset.PosetElement object at 0x10e0bf490>],
[<__main__.Poset.PosetElement object at 0x10e0bf310>, <__main__.Poset.PosetElement object at 0x10e0bf430>, <__main__.Poset.PosetElement object at 0x10e0bf490>],
[<__main__.Poset.PosetElement object at 0x10e0bf310>, <__main__.Poset.PosetElement object at 0x10e0bf370>, <__main__.Poset.PosetElement object at 0x10e0bf490>]]
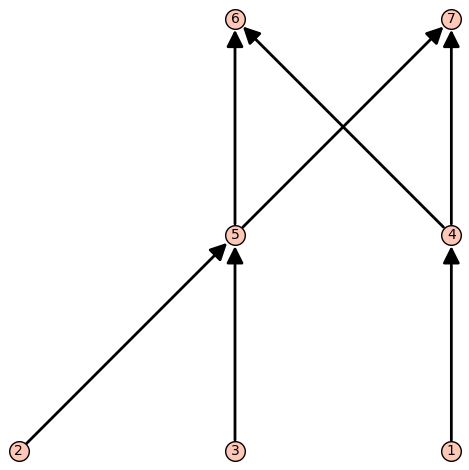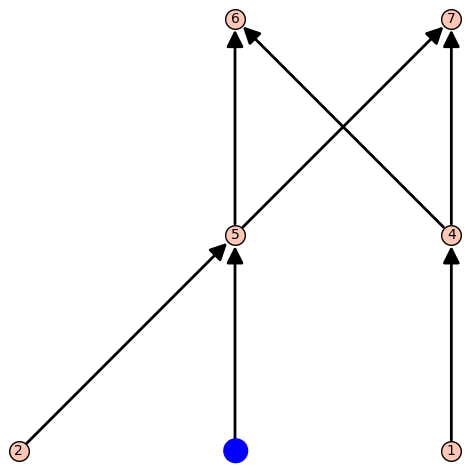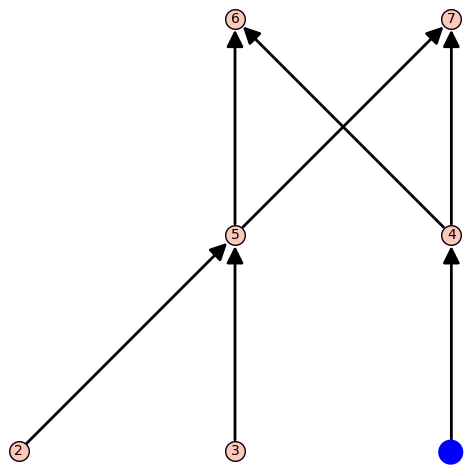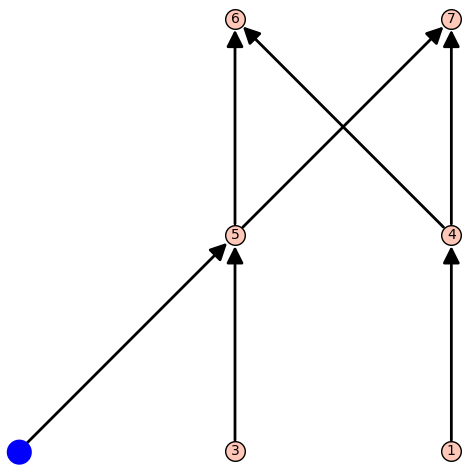
N = Poset([1,2,3,4,5,6,7],[(1,4),(2,5),(3,5),(4,6),(5,6),(5,7),(4,7)])
print(N.maximal_chains(True))
#output:
[[1, 4, 6],[1, 4, 7],[3, 5, 6],[3, 5, 7],[2, 5, 6],[2, 5, 7]]And here's a nice visualization of the algorithms working on the two posets.
Using Our Maximal Chains
Implementing the Depth-First Search algorithm will allow us to get more information about how the elements of our poset are distributed. The first property we'll get is the height of a poset P, which is the length of the longest chain in P. We'll do this by looping over maximal chains.
class Poset():
...
def height(self):
MC = self.maximal_chains(True)
lc = 0
for c in MC:
if len(c) > lc:
lc = len(c)
return lcIn 1972, Haskins and Gudder defined a height function on posets and ever since, it's been a very popular object of study. For example, just a few years later, Kleitman and Rothschild proved that almost all posets have height 3. This means that if we choose a poset "at random" (where we define random appropriately), then that poset will have height 3 with probability 1.
We can adjust what we did slightly and add in an "averaged_height" function which will average the length of all maximal chains in P. I want to round to 2 decimal places, and just for fun, let's do it by multiplying by 100, rounding, and then dividing by 100. This guarantees we only have two decimal places and the last digit is rounded correctly. Probably not too efficient (just use "round(blah,2)" to optimize...)...If written as a math function instead of a Python variable, I'll write a_h for the average height and h for height.
class Poset():
...
def averaged_height(self):
MC = self.maximal_chains(True)
ah = 0
for c in MC:
ah += len(c)
ah = round((ah/len(MC))*100)/100
return ahContinuing with our two example posets:
print(P.height()) #output: 3
print(P.averaged_height()) #output: 3
print(N.height()) #output: 3
print(P.averaged_height()) #output: 2.71We know that "averaged_height" will always be less than or equal to "height". The first example shows equality. When this happens, it means all maximal chains have the same length. A poset P whose maximal chains all have the same length is called a ranked poset and if it also has a unique minimal element (the root), it is called a graded poset because we can assign a grading on the elements defined by their distance from the root.
Studying graded posets can take you all over the wide world of mathematics:
They naturally appear all over number theory
Power sets ordered by inclusion
Set Partitions ordered by refinement
Permutations and Young's Lattice in Representation Theory
Abstract polytopes and simplicial complexes
Whitney Numbers and Hilbert Series in Algebraic Combinatorics
Going back to the averaged height, we already saw
a_h(P) = h(P) if and only if P is a ranked/graded poset
Now what about the other extreme? What if "averaged_height" was MUCH smaller than "height"? If we look at a_h(P)/h(P) as a sliding value from 0 to 1, then 1 represents a very evenly distributed poset while smaller values indicate massively skewed maximal chains.
But how small can it get? As small as we want! If we build a poset P by fixing a single very long chain 1 < 2 < 3 < 4 < ... < k and attaching m outward edges from 1, then h(P) = k, while a_h(P) = (m+k)/(m+1). Therefore
a_h(P)/h(P) = (m+k)/(k(m+1))
If we fixed a long chain of length k, then as m -> ∞, the ratio (m+k)/(m+1) goes to 1, so the overall ratio goes to 1/k, which can be arbitrarily small.
Critical Groups of Graphs
Time for a wonderful detour! After my Sophomore year at James Madison University (2015), I was lucky enough to do an Undergraduate Research project with Dr. James Ducey and my friend Noah Watson on the critical groups (and their variations) of graphs. A beautiful mix of graph theory, group theory, game theory, and dynamics. I won't go into every detail, but here is an overview of what a critical group is.
If we take a graph G = (V,E), then we define a configuration on G to be a labeling of each vertex in V with some integer. If G has n vertices, then the collection of all these labels is just Z^n, where Z is the set of integers. To get the critical group, we define a relation on these labels via a chip-firing game.
If we have a labeling L, we think of L(v) as the number of chips on v. We can fire a vertex v by sending one chip along each edge coming out of v. This decreases the number of chips on v by its degree and increases the number of chips on each neighbor of v by 1. The set of labelings with this relation form a group whose torsion subgroup is the critical group of G.
The linear-algebraic point of view for this is taking the cokernel of the Laplacian Matrix of G, also called the Kirchhoff Matrix. But the chip-firing point of view is much more colorful! We worked directly with configurations of graphs and determined generating configurations so that we could characterize critical groups of certain families of graphs.
Being a torsion subgroup means that the critical group is finite. If we fix a single vertex b as the bank, then we'll let b be negative but force every other vertex to be non-negative. In fact, we'll always have L(b) be the negative of the sum of chips on other vertices so that the total sum of the labelings will be 0. As we fire over and over, eventually we'll land on stable configurations. Take this graph as G:

It is an example of a hinge graph (specifically H(3,2)), whose critical groups are characterized in this paper by Martinian and Vindas-Meléndez. A really nice theorem is that the critical group will always stay the same (formally: isomorphic) regardless of which vertex we choose as bank. For example, fixing 2 as our bank, the configurations we end up with are
(-5,2,2,1), (-4,1,2,1), (-4,2,2,0), (-4,2,1,1)
(-3,0,2,1), (-3,1,2,0), (-3,2,1,0), (-3,2,0,1)
If instead we choose 1 to be our bank, then we get configurations
(-4,1,2,1), (-3,0,2,1), (-3,1,2,3), (-3,1,1,1)
(-2,0,2,0), (-2,0,1,1), (-2,1,1,0), (-2,1,0,1)
So even the bank values are different! But regardless, if you play the chip-firing game, the structure still comes down to Z/8Z. We'll choose 1 as our bank and go ahead and form this group.
The first step we always take is to start at the identity (0,0,0,0) and see which configuration it corresponds to. The dark configurations are the transition ones we get while chip-firing. I'm stopping the chain once we hit our critical configuration the first time, but to confirm it is correct, you'd continue the loop until you hit the configuration a second time.
(0,0,0,0) -> (-3,1,1,1)
So we see that (-3,1,1,1) acts as the identity of our group. Next, we choose another starting point and find the critical configuration it corresponds to, and continue on that way.
(-1,0,1,0) -> (-4,1,2,1)
(-1,1,0,0) -> (--4,2,1,1) -> (-3,0,2,1)
The symmetry of the graph lets us swap (-1,1,0,0) to (-1,0,0,1), which means
(-1,0,0,1) -> (-3,1,2,0)
Next, (-2,1,1,0) maps onto itself, which means (-2,0,1,1) does too, by symmetry. And (-2,1,0,1) and (-2,0,2,0) also map back onto themselves, so that means we found all our critical configurations and we have our critical group!
Making a Poset of Configurations
The idea is simple. We see there are some configurations with the smallest banks and some with the largest. We can get from one extreme to the other just by adding a single chip at a time. If we get from one critical configuration L1 to another L2 by adding a single chip somewhere (and subtracting one from the bank), then we'll say L1 < L2. This forms a poset structure!
And the first cool thing is that even though the choice of bank doesn't affect the critical group, it does affect this poset! Finally ready for pictures, here are the two sets of configurations we found above but organized into this poset structure. First, we'll set the bank equal to 2.

Next, we'll look at the poset when our bank is 1.

There are some things that stay the same when changing the bank and some things that don't. Often this poset encodes the automorphism group of G, which in my opinion makes it an interesting thing to study. Plus, maybe you can tell I enjoy posets. That summer, we spent a good week or so exploring various properties of these posets, but we never ended up doing anything with it. Maybe I'll try to explore some of their properties later with our Poset class!
For now, let me list a few of the results we did prove. First we give some definitions:
The Whitney numbers of a graded poset P, denoted W(P,i), are the number of elements of P that have rank = i.
The automorphism group of a graph G, denoted Aut(G), is the group of all maps from V to V that preserve adjacency AND non-adjacency.
A configuration is stable if there are no vertices with enough chips to fire. When we hit a stable configuration, we fire the bank and then continue.
A configuration is recurrent if our chip-firing brings us into a loop containing that configuration.
A configuration is critical if it is both stable and recurrent, meaning it is the unique stable configuration in the final loop we end up in while chip-firing.
Ok, so here are a few cool things we discovered about these posets!
If G is vertex--transitive, then there is only one poset P(G) up to isomorphism. The converse is not true, and the bow-tie graph is a counterexample.
If C is a critical configuration and d another configuration, then C + d being stable means that C + d is critical.
For any graph G and any bank vertex, the poset will have a unique maximal configuration with exactly one less chip on each vertex than is needed to fire.
The minimum value of the bank b is deg(b) - |E|, where E is our edge set.
The last two points mean that the height of our poset is |E| - |V| + 2.
If C is a minimal configuration in our poset, then its bank is deg(b) - |E|.
The number of minimal configurations in the poset formed from the critical group of the Wheel Graph W_n is 2^n - 2. (This one we were really happy with!)
And some conjectures we noted:
If there is an automorphism that sends one vertex to another, then the two posets with those vertices as the bank are isomorphic.
The Whitney Numbers of the Friendship Graph FG(n,k) have generating function
(1 + nx)^k.
3. Inspired by the previous point, if F1 and F2 are the generating functions for the Whitney numbers of G1 and G2, then the wedge product of G1 and G2 at a single vertex has generating functions F1*F2.
That was fun to look back on! Next time, maybe we'll think about building a Graph class?
Thank you for reading!
Jonathan M Gerhard





Comments