An introduction
If you've done calculus, then you've talked about differentiation. We usually talk about this in terms of "linear approximations" and "limit definitions" to try to understand functions of a real variable - those smooth curves we can draw nicely, like polynomials or exponential functions.
But who says we should only look at those?
We can view differentiation as an operator D on the space of smooth functions C, meaning that D takes a smooth function to another smooth function - its derivative. We write this as
D: C -> C
But I like COUNTING things. So I don't want to work with (uncountably) infinitely many smooth functions, let's just work with the nicer (countably infinite) set of natural numbers:
N = {0,1,2,3,...}
The most important rule related to differentiation is Leibniz's Product Rule:
D(fg) = fD(g) + D(f)g
But we don't want functions f,g anymore - we want to view D as an operator on the natural numbers instead! So let's replace f and g with natural numbers a and b to define
D: N -> N
by
D(ab) = aD(b) + D(a)b
But this doesn't quite help us when our number isn't the product of two other numbers! So we need to also define the initial conditions on what D does to 0, 1:
D(0) = 0
D(1) = 0
D(p) = 1 for all prime numbers p.
Now that we've got this basis, we can start computing some derivatives!
D(4) = D(2*2) = 2D(2) + D(2)2 = 2 + 2 = 4
D(6) = D(3*2) = 3D(2) + D(3)2 = 3 + 2 = 5
D(8) = D(4*2) = 4D(2) + D(4)2 = 4 + 8 = 12
D(9) = D(3*3) = 3D(3) + D(3)3 = 3 + 3 = 6
Now that we have a few examples, let's make a table of the first 21 natural numbers!
n (natural number) | D(n) (derivative of n) |
|---|---|
0 | 0 |
1 | 0 |
2 | 1 |
3 | 1 |
4 | 4 |
5 | 1 |
6 | 5 |
7 | 1 |
8 | 12 |
9 | 6 |
10 | 7 |
11 | 1 |
12 | 16 |
13 | 1 |
14 | 9 |
15 | 8 |
16 | 32 |
17 | 1 |
18 | 21 |
19 | 1 |
20 | 24 |
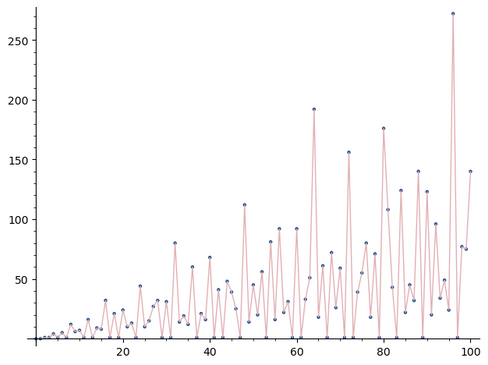
And for more fun, here is a graph of the derivatives of the numbers 0 through 100.
The first has consecutive numbers connected by a straight line and the second is just the points.
In the next few posts, I'm going to be asking many questions about the arithmetic derivative and the patterns we can find. I'll be able to answer some of these and certainly will NOT be able to answer most of them. But either way, it will be interesting!
Questions for next time
What application does this have to the rest of math? (Proof that sqrt(2) is irrational)
What's a fixed point of the arithmetic derivative? (When is D(n) = n)
Can we solve other equations D(n) = m?
Thank you for reading!
Jonathan Gerhard